Does changing the shape of an object change its volume?
Plan Investigating Volume 3
What if you had a bucket of sand, and you made a sandcastle with it. What would happen if you scooped up all that sand and made a sand dragon instead? Would the dragon have the same volume as the castle?
Formative Assessment
Available online at inquiryproject.terc.edu
In this investigation, students grapple with the idea that volume can remain constant when an object changes its shape. First they arrange eight wooden cubes into different shapes and determine that the volumes of the different objects are the same. Then they repeat the activity using plastic modeling clay.
As they squeeze and poke the plastic modeling clay into irregular shapes — and can no longer count the cubes — they are left to wonder: Same volume or different?
Learning Goals
- to consider whether changing the shape of an object also changes its volume
| Sequence of experiences | ||
|---|---|---|
| 1. Ask the question | Small Groups | 15 Mins |
| 2. Explore shape and volume with wooden cubes | Small Groups | 10 Mins |
| 3. Explore shape and volume with plastic modeling clay cubes | Small Groups | 20 Mins |
| 4. Make meaning | All Class | 10 Mins |
Materials and Preparation
For the class:- Post the investigation question in a place where all students can see it
- Class volume line from the previous sessions
- 1 plastic knife
- 1 small plate
- 8 centimeter cubes
- Approximately 10 cubic centimeters of plastic modeling clay
Concept Cartoon

The Volume Concept Cartoon is typically used as a formative assessment at the end of this investigation.
Do students understand that the volume of 8cc of plastic modeling clay stays the same even if you change the shape?
Listen to the students' discussion of their new 8cc plastic modeling clay shapes as evidence of their current understanding of volume. Joan listens for these ideas as she interprets their responses to her questions. Note that all the sculptures on Joan's tray have the same 8cc volume.
- The volume is the same even if you change the shape, because you haven't added any plastic modeling clay or taken any away.
- Even though the shapes look different, the volume of the plastic modeling clay is still the same - 8 ccs.
- The volumes are not the same because the new shape looks like it takes up more space (inaccurate).
As a next step, Joan shows a tray holding all of the 8cc objects and asks, "If I made a volume line, where would we put each of these objects?"
1. Ask the question
Drawing attention to the objects arrayed on the class volume line:
- How is volume different from shape?
It’s a tricky distinction, and students may struggle with it. What responses do they have? Encourage different formulations until you reach a consensus like this:
- Shape describes what an object looks like, or how it is arranged. Volume describes how much space it takes up.
Check for understanding:
- Can two objects have the same shape but have different volumes?
- Yes, for example a small cube and a large cube.
Once the class is clear about the distinction between shape and volume, introduce the investigation question:
What about compressible materials? This investigation deals with incompressible materials like wooden blocks. Simply rearranging the blocks into different shapes will not change their volumes. Compressible materials behave differently. For example, when you squeeze a slice of Wonder Bread, it loses volume.
Help them with the inquiry by presenting some scenarios:
- Say you made a robot out of 300 Lego pieces. What if you took the robot apart and made a spaceship instead, using all the Legos. Do you think the robot and the spaceship have different volumes?
- What if you and your best friend each have a liter of milk. If you pour all your milk into a big jar, and your friend pours all his milk into 16 glasses, who has more milk?
- Say you had a wall made of bricks. If you tore it down and built a whole different wall, using all the same bricks, would the new wall have the same volume as the old wall? Let’s find out.
2. Explore shape and volume with wooden cubes
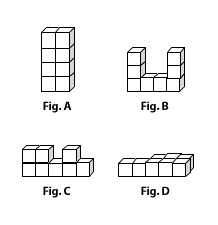
Explore: Start the exploration by distributing eight centimeter cubes to each student. Do they remember that each cube has a volume of 1 cubic centimeter? Have each student construct a rectangle–shaped building that is four cubes (or four “stories”) tall and two cubes wide (see Figure A). When everyone has finished, ask a volunteer to describe the volume. If necessary, remind the class that the volume can be found by counting the cubes.
Predict: Now ask the students to predict what the volume will be if they rearrange the eight cubes into a different shape. They should record their predictions in their notebooks.
Explore: At each table, have one student construct a new four–story building, one construct a three–story building, one construct a two–story building, and one construct a one–story building (see Figures B, C, and D for examples); each building must use all eight cubes. Students should record the volume of their new building in their notebooks. Ask students to report on the volume of their new buildings.
Is there agreement that the volume remains the same, i.e., 8 cubic centimeters, or are there different opinions? Ask students to show you the method they used for determining the new volume. Is everyone focused on volume, or are some thinking about area, perimeter, length, or height? Drawing attention again to the investigation question:
3. Explore shape and volume with plastic modeling clay cubes
Students continue to explore the investigation question, this time using a different material: plastic modeling clay.

Give each student approximately 10 cubic centimeters of plastic modeling clay. Have students use their plastic knife to help them shape the plastic modeling clay into eight individual centimeter cubes. They can use the wooden cubes as models.
As they finish, have students return the excess plastic modeling clay to a central location.
Check understanding:
- How much plastic modeling clay do you have?
- 8 centimeter cubes = 8 cubic centimeters
Tell students that they now have a new challenge: To create a new building, this time using their plastic modeling clay cubes. There are just two rules:
- They must use all eight cubes
- They must keep four of the cubes in cube shape, but they can change the shape of the other four cubes in any way they please.

Point out that since the plastic modeling clay cubes stick together — and can be squeezed and poked — students will be able to make shapes that were not possible when they were using the wooden cubes.
As they finish, have students place their constructions on a large piece of paper in the class meeting area and gather there for discussion.
4. Make meaning
Purpose of the discussion

This class built 10 cubic centimeter shapes.
This discussion will bring forward students’ ideas about volume. When 8 cubic centimeters of plastic modeling clasy are reshaped, does the volume stay the same or change? You may want to review The Challenges of Learning About Volume. It’s easy to underestimate the challenges presented as students begin to learn about volume. In this discussion, listen carefully to students’ ideas. Provide plenty of “wait time” so you and your students can make sense of the conversation. In this discussion, encourage students to support their position (no, the volume doesn’t change or yes, it does) with evidence and reasoning.
Deep understanding of volume develops over time. If a student’s understanding of volume seems fragile at this point in time, remember that this concept will be revisited and is a focus of the 4th grade curriculum.
Revisit the activities the students have just completed
Remind students where they began: making different arrangements with their 8 centimeter cubes and deciding that the volume was always 8 cubic centimeters — they hadn’t added any cubes or taken any away. Then they made their own centimeter cubes out of plastic modeling clay, put them together, changed the shape of some of them, and wondered if the volume was the same or different.
Engage students in the focus question
Does changing the shape change the volume?
- The volume has to be the same because we haven't added any plastic modeling clay or taken any away.
- If we turned the plastic modeling clay back into centimeter cubes, there would be 8 of them so the volume hasn't changed.
- I made 4 of the cubes into a ball and my object looks bigger now so there is more volume.
Supporting questions
- If you took the plastic modeling clay in your rabbit (new shape) and reshaped it back into cubes, what do you think you would find?
- What was the volume of your original 8 plastic modeling clay centimeter cubes?
- Did you add any plastic modeling clay to your original 8 cubic centimeters or take any away?
Recap the discussion
Summarize the idea that volume is the amount of space an object takes up. As long as we don’t add any material or take any away, the volume will stay the same even if we change the shape of the object.