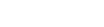Weight
The weight of an object is related to the amount of matter in the object, ultimately how many protons, neutrons, and electrons it consists of. And weight is conserved: in a closed system, it doesn’t change. But what do young children think? Do they believe that all material objects have weight? Do they view weight as a fine-grained measure having a wide range of possible values?
To develop a sound understanding of matter, students need to embrace the idea that matter consists of tiny particles having properties that cannot be directly observed.
Prior research has suggested children view weight as closely tied to their own direct experience (“felt weight”). Accordingly, objects that feel like they have no weight must have no weight at all. And the number of possible weights corresponds to the number of weights that one can personally discriminate.
Does a little speck of clay have weight or take up space?
We asked children to think and reason about tiny things, including those too small to be seen or felt.
At the beginning of grade 3 (see Figure 2), about 90% of the students in our sample claimed that a tiny visible speck of clay (removed from a larger ball of clay they had already acknowledged as having weight) weighed nothing at all. Over half of these denied that the speck took up any space. Almost 40% of the students thought it took up space but weighed nothing at all. Fewer than one in ten thought the visible speck both took up space and had weight.

Figure 2: Judgments about tiny visible specks. Responses are from treatment students (grade 3 pre and post) and control students (end of grade 3).
Children were also asked if there could be a piece of clay too small to see, and, if so, whether that (invisible) piece would take up space or have weight. The pattern of responding about invisible pieces was very similar (see Figure 3). For young third graders: over 50% either denied the existence of an invisible piece or said the invisible piece took up no space and had no weight, 40% said it only took up space or had weight (but not both), and 7% said it both took up space and had weight.
For most third graders it was easier to admit the existence of invisibly small pieces than to claim they occupied space and had weight.
The 3rd grade Inquiry Curriculum had provided direct support for developing new ways of thinking about weight that go beyond perceptual appearances (see Wiser, Smith, Asbell-Clarke, & Doubler, 2009 for more details). In comparing their own judgments of weight with the results of a balance scale, students discussed the strengths and limits of their senses. They also learned to use measurements to compare the weights of objects and to use weight line representations. In addition, they used their weight line representations to consider what happens to the weight of a 4g object (clay piece) that is repeatedly divided in half. Would you ever get to zero?
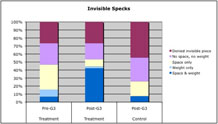
Figure 3. Comparison of the patterns of judgment on the Invisible Specks questions for the treatment students (grade 3 pre and post) and control students (end of grade 3).
Instruction made a difference. During Grade 3, the percent of treatment students claiming that a small speck of clay has weight and takes up space jumped from less than 10% to 60% (Figure 1). In contrast, the control students (interviewed at the end of grade 3) were still responding as the Treatment students had at the beginning of grade 3. Striking and significant differences between Treatment and Control were maintained at Grade 4 and 5 as well.
The granularity of weight: How many weights are there between the weight of a large and small ball?
In a Granularity of Weight subtask, children are given two clay balls; the volume and weight of the larger ball is three times as great as that of the smaller ball. The student is asked if she can make a ball of clay having a weight falling in between those of the larger and smaller balls (see Figure 4).

Figure 4. The two clay balls used in the Granularity of Weight task: the larger pink ball (120 g) and the smaller green ball (40 g).
Approximately 4 out of 5 third graders claimed very few weights (generally only 1, 2, or 3) could exist that are greater than that of the small ball and larger than that of the larger ball. Some children (about 10-15%) suggest there may more than a dozen. But only exceptionally (2-3% of the time) do young students suggest that the number of possible distinct weights in the interval is enormous ("lots and lots", "infinite", "goes on and on"). There were no differences between treatment and control students in their answers on these questions at the end of grade 3.
Children made a little progress on these questions, across grades 4 and 5. By grade 5, approximately 20% of Treatment and 17% of Control students realized that the number of weights between the two balls was “uncountably large.” Still, the majority of students thought there were only a small finite number of weights (less than 12), and there were no differences between the Treatment and Control.
Our findings suggest that it may be easier for children to attribute weight to imperceptibly tiny objects than to acknowledge unnoticeable differences in weight among relatively large objects.
Students were familiar with the expression between (or in-between) as connoting an intermediate position (located between A and B). However, some found the idea of an intermediate weight puzzling. They realized of course that weights come in different values (as do other properties). And they knew that relative magnitudes can be compared (bigger, smaller, equal in magnitude), generally, two at a time. But a statement such as, “this weight is in between the weight of the other two” is predicated on a convention under which positions along a line denote different magnitudes, and displacements in one direction correspond to monotonic increases (or decreases) in value. The convention is adopted in modern science for measurable quantities whenever axes, number lines, or measure lines are used to represent physical quantities.
When an interviewer sensed that a student was having trouble with the metaphoric sense of in-between or confusing it with its literal interpretation, he described what he was looking for was a ball that was “heavier than the small ball” but “not as heavy as the large ball”. This may have sufficed to get through the momentary glitch in the interview. However, it would be a long-term matter for students to fully adopt the convention of treating measures as axes and continua. And this was one of the reasons that measure lines figure heavily in the Inquiry curriculum.