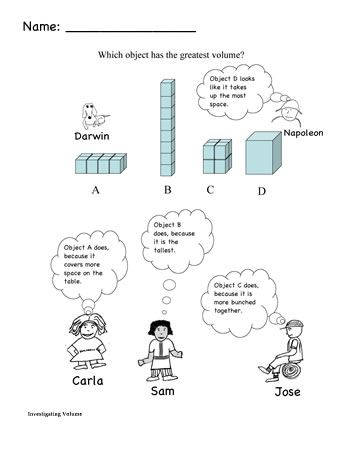
Volume Concept Cartoon
This cartoon was developed to probe students’ understanding of volume as a 3–dimensional measure of the amount of space an object occupies. At issue is whether students differentiate volume from area or length, whether they see the small cubes as units of volume measure, and whether they realize measures require standard size units. It is typically used after Investigating Volume 3, Does changing the shape of an object change its volume?.
Things to look for in student responses
How do students use the information in the drawings to make inferences about the volume of the objects (in the data table)?
Some children may confuse volume with area, agree with Carla, and infer the volume of A is 8 squares, B is one square, and C is 4 squares.
Others may confuse volume with length, agree with Sam, and infer the volume of A is 4, B is 8, and C is 2.
Still others will “count the cubes” and conclude that A, B, and C have the same volume of 8 small cubes. (Of course, if these students only count “visible” cubes they may erroneously think C has only 6 or 7.) For the latter group of students (who attempt to “count the cubes”) it is of great interest what they infer for D, whether they give only numeric values or units, and how they describe the units.
- Some students may mistakenly give D a value of 1 cube, showing when they count the cubes it does not matter what size they are.
- Others may simply say D has a volume greater than 8 cubes (noting the comparison with C and the fact that it is bigger in all dimensions) or give some wildly bigger number, such as 30.
- Still others may attempt to partition D into cubes and estimate its volume (estimating it has a volume of about 10-12 cubes). Some students may talk of the cubes as “cubic centimeters” while others simply refer to them as cubes.
Do students draw on the information in their data table in making arguments about which character they agree with?
Some students may view filling out the data table as an independent exercise. Others will make arguments that draw on the analysis provided, arguing that either A, B, C, or D has the greatest volume as noted above.