Does changing the shape of an object change its volume?

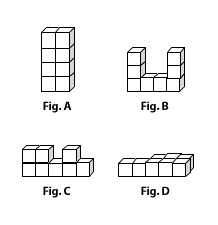
Explore: Start the exploration by distributing eight centimeter cubes to each student. Do they remember that each cube has a volume of 1 cubic centimeter? Have each student construct a rectangle–shaped building that is four cubes (or four “stories”) tall and two cubes wide (see Figure A). When everyone has finished, ask a volunteer to describe the volume. If necessary, remind the class that the volume can be found by counting the cubes.

Predict: Now ask the students to predict what the volume will be if they rearrange the eight cubes into a different shape. They should record their predictions in their notebooks.

Explore: At each table, have one student construct a new four–story building, one construct a three–story building, one construct a two–story building, and one construct a one–story building (see Figures B, C, and D for examples); each building must use all eight cubes. Students should record the volume of their new building in their notebooks. Ask students to report on the volume of their new buildings.

Is there agreement that the volume remains the same, i.e., 8 cubic centimeters, or are there different opinions? Ask students to show you the method they used for determining the new volume. Is everyone focused on volume, or are some thinking about area, perimeter, length, or height? Drawing attention again to the investigation question: